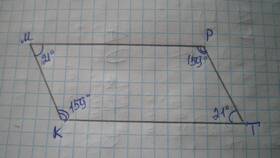
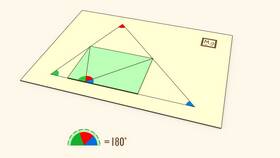
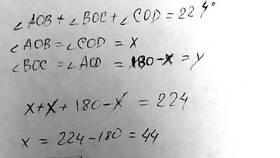Сумма трех углов может иметь разные значения в зависимости от контекста и геометрической фигуры, о которой идет речь. Рассмотрим основные случаи, с которыми можно столкнуться в геометрии.
Содержание
Сумма углов треугольника
Наиболее известный случай в планиметрии - сумма внутренних углов треугольника:
- В евклидовой геометрии (на плоскости) сумма трех углов треугольника всегда равна 180°
- В сферической геометрии сумма углов превышает 180°
- В гиперболической геометрии сумма углов меньше 180°
Пример расчета для плоского треугольника
| Угол A | 60° |
| Угол B | 70° |
| Угол C | 50° |
| Сумма | 180° |
Сумма трех углов в других фигурах
Четырехугольник
Сумма любых трех углов выпуклого четырехугольника всегда меньше 360° (так как сумма всех четырех углов равна 360°)
Многоугольник
Для n-угольника сумма трех углов будет составлять часть от общей суммы (n-2)×180°
Сумма трех углов в пространстве
Трехгранный угол
В стереометрии сумма плоских углов трехгранного угла всегда меньше 360°
| Тип трехгранного угла | Сумма плоских углов |
| Острый | Меньше 270° |
| Прямой | Меньше 360° |
| Тупой | Меньше 540° |
Практическое применение
Знание суммы углов используется в:
- Архитектуре и строительстве
- Геодезии и картографии
- Компьютерной графике
- Навигационных системах
- Решение геометрических задач
Заключение
Сумма трех углов не является постоянной величиной и зависит от геометрической системы и типа фигуры. В классической планиметрии сумма углов треугольника составляет 180°, что служит основой для многих геометрических теорем и практических расчетов. Для других случаев необходимо учитывать специфику конкретной геометрической системы.