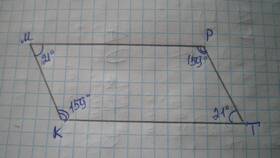
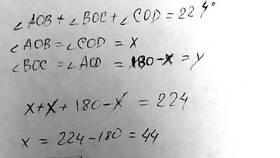Сумма двух углов зависит от их типа и взаимного расположения. В геометрии существуют различные случаи, когда сложение углов дает определенные результаты. Рассмотрим основные ситуации.
Содержание
Основные случаи сложения углов
| Тип углов | Сумма | Пример |
| Два острых угла | Менее 180° | 30° + 45° = 75° |
| Два прямых угла | 180° | 90° + 90° = 180° |
| Два тупых угла | Более 180° | 100° + 110° = 210° |
| Острый и тупой угол | Зависит от значений | 60° + 120° = 180° |
Специальные случаи сложения углов
Смежные углы
Два угла называются смежными, если у них одна сторона общая, а другие стороны составляют прямую линию. Сумма смежных углов всегда равна 180°.
Вертикальные углы
Вертикальные углы равны между собой, но их сумма зависит от конкретных значений. Например, два вертикальных угла по 45° дадут в сумме 90°.
Углы треугольника
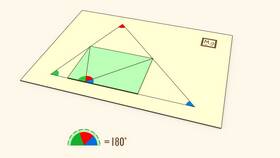
Сумма любых двух углов треугольника всегда меньше 180°, так как сумма всех трех углов треугольника равна 180°.
Практические примеры вычислений
- Если первый угол равен 35°, а второй 55°, их сумма составит 90° (прямой угол)
- При сложении углов 120° и 60° получаем 180° (развернутый угол)
- Сумма углов 15° и 25° равна 40° (острый угол)
- Два угла по 135° дадут в сумме 270° (превышение полного оборота)
Важные свойства суммы углов
- Максимальная сумма двух углов на плоскости - 360°
- Минимальная сумма - 0° (для нулевых углов)
- Сумма двух углов может быть больше 360°, если рассматривать углы поворота
- В сферической геометрии суммы углов ведут себя иначе, чем на плоскости
Применение в задачах
Знание суммы углов используется при решении различных геометрических задач:
| Тип задачи | Как применяется |
| Нахождение третьего угла треугольника | 180° минус сумма двух известных углов |
| Доказательство параллельности прямых | Через сумму внутренних односторонних углов |
| Построение геометрических фигур | Расчет необходимых углов для построения |
Заключение
Сумма двух углов может принимать различные значения в зависимости от их величины и взаимного расположения. На плоскости эта сумма всегда находится в пределах от 0° до 360°. Понимание принципов сложения углов является фундаментальным для изучения геометрии и решения практических задач в различных областях науки и техники.