Теорема о сумме углов треугольника утверждает, что сумма внутренних углов любого треугольника равна 180 градусам. Рассмотрим несколько способов доказательства этой фундаментальной геометрической теоремы.
Содержание
Классическое доказательство через параллельные прямые
- Пусть дан произвольный треугольник ABC
- Проведем через вершину B прямую DE, параллельную стороне AC
- Угол DBA равен углу BAC как накрест лежащие при параллельных DE и AC и секущей AB
- Угол EBC равен углу BCA как накрест лежащие при тех же параллельных и секущей BC
- Углы DBA, ABC и EBC образуют развернутый угол, равный 180°
- Следовательно, ∠A + ∠B + ∠C = 180°
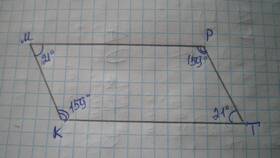
Доказательство с использованием свойств параллелограмма
| Шаг | Действие |
| 1 | Построим параллелограмм ABCD на стороне AB треугольника ABC |
| 2 | Продолжим сторону AC до пересечения с продолжением стороны BD в точке E |
| 3 | Углы при вершине C треугольника ABC равны соответствующим углам при вершине E |
| 4 | Сумма углов в точке E составляет 180° |
| 5 | Следовательно, сумма углов треугольника ABC также равна 180° |
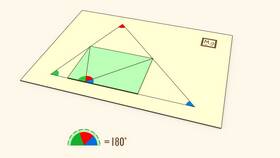
Практическое доказательство методом отрывания углов
- Нарисуйте треугольник на бумаге и вырежьте его
- Аккуратно оторвите все три угла треугольника
- Совместите оторванные углы вершинами в одной точке
- Убедитесь, что они образуют прямую линию (180°)
Доказательство через сумму углов многоугольника
Формула суммы внутренних углов n-угольника: S = (n-2) × 180°
Для треугольника (n=3): S = (3-2) × 180° = 180°
Дополнительные методы доказательства
- Сферическая геометрия: На сфере сумма углов треугольника превышает 180°
- Гиперболическая геометрия: В пространстве Лобачевского сумма углов меньше 180°
- Координатный метод: Использование скалярного произведения векторов
Историческая справка
| Математик | Вклад |
| Евклид | Первое известное доказательство в "Началах" (300 г. до н.э.) |
| Прокл | Альтернативное доказательство через параллельные прямые |
| Лежандр | Доказательство для сферических треугольников |
Применение теоремы в геометрии
- Вычисление неизвестных углов треугольника
- Доказательство равенства треугольников
- Построение геометрических фигур
- Решение задач на подобие треугольников
Заключение
Теорема о сумме углов треугольника является одной из основополагающих в евклидовой геометрии. Различные методы доказательства этой теоремы демонстрируют глубину геометрических взаимосвязей и служат прекрасным примером математической красоты и логики.